基尔霍夫电路定律(Kirchhoff Circuit Laws)简称为基尔霍夫定律,指的是两条电路学定律,基尔霍夫电流定律与基尔霍夫电压定律。它们涉及了电荷的守恒及电势的保守性。1845年,古斯塔夫·基尔霍夫首先提出基尔霍夫电路定律。现在,这定律被广泛地应用于电机工程学。
从麦克斯韦方程组可以推导出基尔霍夫电路定律。但是,基尔霍夫并不是依循这条思路发展,而是从格奥尔格·欧姆的工作成果加以推广得之。
所有进入某节点的电流的总和等于所有离开这节点的电流的总和。
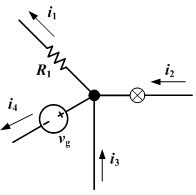
所有进入节点的电流的总和等于所有离开这节点的电流的总和。对于本图案例,i1 + i4 = i2 + i3 。
以方程表达,对于电路的任意节点,
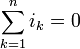 ;
;
其中,ik 是第 k 个进入或离开这节点的电流,是流过与这节点相连接的第 k 个支路的电流,可以是实数或复数。
基尔霍夫电流定律又称为基尔霍夫第一定律。由于累积的电荷(单位为库仑)是电流(单位为安培)与时间(单位为秒)的乘积,从电荷守恒定律可以推导出这条定律。
[编辑] 导引
思考电路的某节点,跟这节点相连接有 n 个支路。假设进入这节点的电流为正值,离开这节点的电流为负值,则经过这节点的总电流 i 等于流过支路 k 的电流 ik 的代数和:
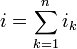 。
。
将这方程积分于时间,可以得到累积于这节点的电荷的方程:
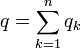 ;
;
其中,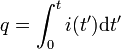 是累积于这节点的总电荷,
是累积于这节点的总电荷,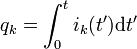 是流过支路 k 的电荷,t 是检验时间,t' 是积分时间变量。
是流过支路 k 的电荷,t 是检验时间,t' 是积分时间变量。
假设 q > 0 ,则正电荷会累积于节点;否则,负电荷会累积于节点。根据电荷守恒定律, q 是个常数,不能够随着时间演进而改变。由于这节点是个导体,不能储存任何电荷。所以,q = 0 、i = 0 ,基尔霍夫电流定律成立:
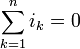 。
。
[编辑] 含时电荷密度
从上述推导可以看到,只有当电荷量为常数时,基尔霍夫电流定律才会成立。通常,这不是个问题,因为静电力相斥作用,会阻止任何正电荷或负电荷随时间演进而累积于节点,大多时候,节点的净电荷是零。
不过,电容器的两会导板可能会允许正电荷或负电荷的累积。这是因为电容器的两块导板之间的空隙,会阻止分别累积于两块导板的异性电荷相遇,从而互相抵消。对于这状况,流向其中任何一块导板的电流总和等于电荷累积的速率,而不是零。但是,若将位移电流 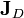 纳入考虑,则基尔霍夫电流定律依然有效。详尽细节,请参阅条目位移电流。只有当应用基尔霍夫电流定律于电容器内部的导板时,才需要这样思考。若应用于电路分析(circuit analysis)时,电容器可以视为一个整体元件,净电荷是零,所以原先的电流定律仍适用。
纳入考虑,则基尔霍夫电流定律依然有效。详尽细节,请参阅条目位移电流。只有当应用基尔霍夫电流定律于电容器内部的导板时,才需要这样思考。若应用于电路分析(circuit analysis)时,电容器可以视为一个整体元件,净电荷是零,所以原先的电流定律仍适用。
由更技术性的层面来说,取散度于麦克斯韦修正的安培定律,然后与高斯定律相结合,即可得到基尔霍夫电流定律:
 ;
;
其中,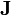 是电流密度,ε0 是电常数,
是电流密度,ε0 是电常数,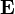 是电场,ρ 是电荷密度。
是电场,ρ 是电荷密度。
这是电荷守恒的微分方程。以积分的形式表述,从封闭表面流出的电流等于在这封闭表面内部的电荷 Q 的流失率:
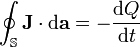 。
。
基尔霍夫电流定律等价于电流的散度是零的论述。对于不含时电荷密度 ρ ,这定律成立。对于含时电荷密度,则必需将位移电流纳入考虑。


 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底